Example 1: Continuous Surrogate Marker • OptimalSurrogate

library(OptimalSurrogate)

Load data with a continuous surrogate marker. Take a look at first few and last few rows. Note that sob indicates the surrogate marker value, yob is the value of the primary outcome, and aob is the treatment indicator (0 or 1).

data(marker_cont)
head(marker_cont)

##        sob yob aob
## 1 1.661730   1   0
## 2 7.141513   0   0
## 3 3.889047   0   1
## 4 4.101624   1   0
## 5 7.770818   0   0
## 6 9.207453   1   1

tail(marker_cont)

##           sob yob aob
## 995  6.353809   1   0
## 996  7.337931   0   1
## 997  4.519351   0   1
## 998  3.342114   0   0
## 999  8.015779   1   0
## 1000 7.085481   1   1

Run function pte_cont which is the main function for a continuous surrogate marker. You must indicate which variable is the surrogate, primary outcome and treatment, whether standard error estimates are desired (var = TRUE), whether confidence intervals are desired (conf.int=TRUE), and the number of replications to be used for resampling (used to estimate variance and confidence intervals; default is 500).

set.seed(123)
system.time(out <- pte_cont(
  sob = marker_cont$sob, 
  yob = marker_cont$yob, 
  aob = marker_cont$aob, 
  var = TRUE, conf.int = TRUE, rep = 1000))

##    user  system elapsed 
##  13.084   1.530  14.679

out[[1]]

##                 est         se      lower      upper
## delta    -0.2412751 0.03130459 -0.3026321 -0.1799181
## delta.gs -0.1597523 0.02009536 -0.1991392 -0.1203654
## pte1      0.6621168 0.05840355  0.5476459  0.7765878
## pte2      0.4927234 0.02680243  0.4401906  0.5452562

x <- as.numeric(rownames(out[[2]]))
plot(x, out[[2]][, "est"], ylim = range(out[[2]][, -2]), type = "l", 
     las = 1, xlab = "Surrogate Marker", ylab = "Optimal Transformation")
  lines(x, out[[2]][, "lower"], lty = 2)
  lines(x, out[[2]][, "upper"], lty = 2)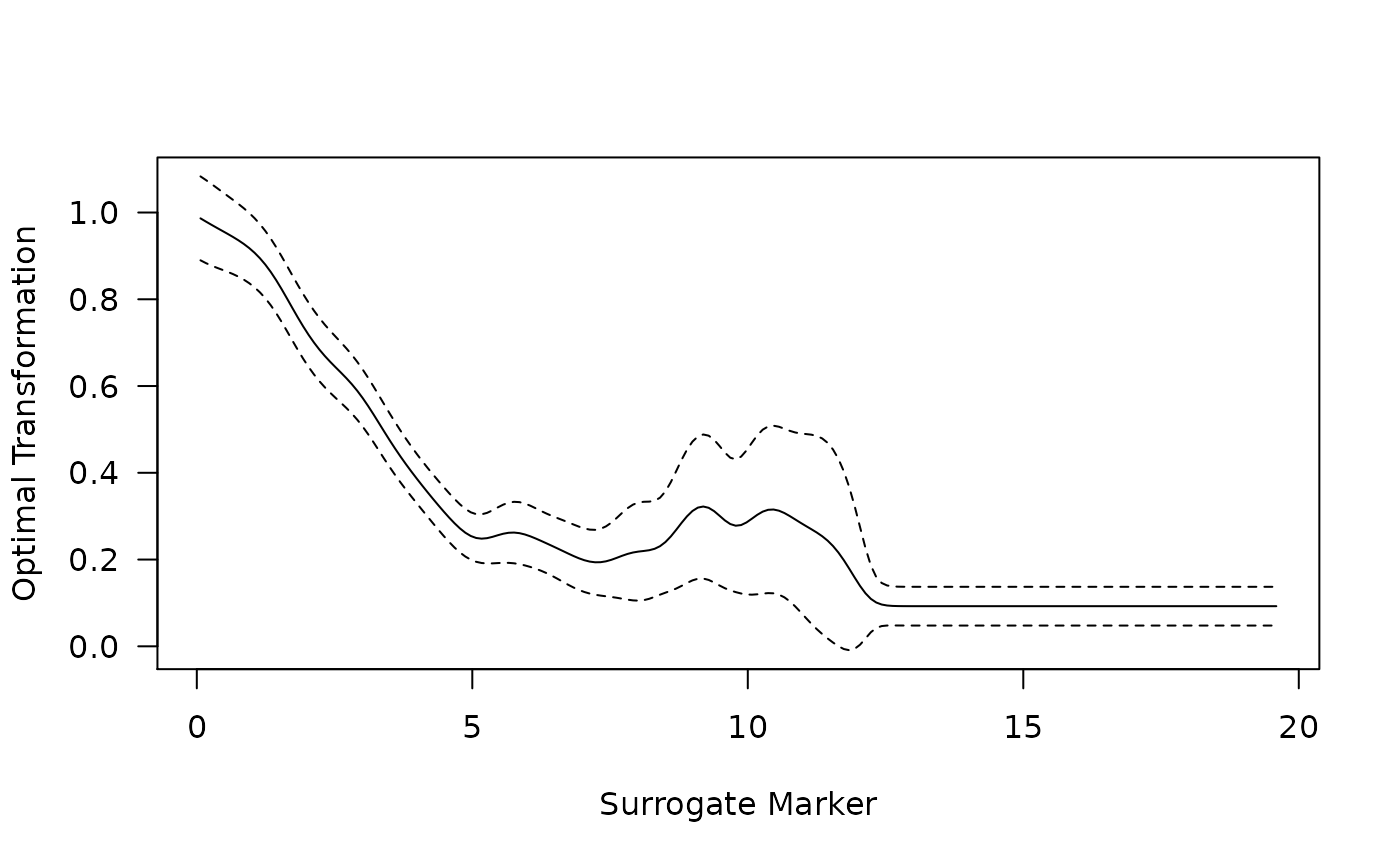

The function outputs estimates (and standard error estimates and confidence intervals if indicated) of \(\Delta\), the true treatment effect; \(\Delta_{g_{opt}(S)}\), the treatment effect on the optimal transformation of the surrogate denoted as \(g_{opt}(S)\); \(PTE_1 =\Delta_{g_{opt}(S)} / \Delta\), a version of the proportion of treatment effect explained quantity based on the ratio between the treatment effect on the optimal transformation of the potential surrogate marker and the treatment effect on the primary outcome; and \(PTE_2\) a version of the proportion of treatment effect explained quantity based on quantifying how well the individual-level treatment effect on the primary outcome can be approximated by the effect on the identified optimal transformation.

Here, the treatment effect is estimated to be -0.24, and the treatment effect on the optimal transformation of the surrogate is estimated to be -0.16. The resulting proportion of treatment effect estimates are 0.66 using \(PTE_1\) and 0.49 using \(PTE_2\). These results indicate that this is a poor-to-moderate surrogate marker in this setting.